Mathematical Olympiad Problems And Solutions Pdf

42nd International Mathematical Olympiad

Now consider a 21 × 21 grid, with one side representing girls, the other boys. Each cell in the grid is filled with the problems solved by both the corresponding boy and girl. There are at most 6 problems in each row and each column and each cell must contain at least one problem. In each row R i there is problem P i that appears at least three times.

10 Baca lebih lajut

A Collection of Problems Suggested for the International Mathematical Olympiads: 1959–2004

The book is organized as follows. For each year, the problems that were given on the IMO contest are presented, along with the longlisted and/or shortlisted problems, if applicable. We present solutions to all shortlisted problems. The problems appearing on the IMOs are solved among the other shortlisted problems. The longlisted problems have not been provided with solutions, except for the two IMOs held in Yugoslavia (for patriotic reasons), since that would have made the book unreasonably long. This book has thus the added benefit for professors and team coaches of being a suitable book from which to assign problems. For each problem, we indicate the country that proposed it with a three-letter code. A complete list of country codes and the corresponding countries is given in the appendix. In all shortlists, we also indicate which problems were selected for the contest. We occasionally make references in our solutions to other problems in a straightforward way. After indicating with LL, SL, or IMO whether the problem is from a longlist, shortlist, or contest, we indicate the year of the IMO and then the number of the problem. For example, (SL89-15) refers to the fifteenth problem of the shortlist of 1989.

Baca lebih lanjut

749 Baca lebih lajut

The 53rd International Mathematical Olympiad: Problems and Solutions

At the start of the game the player chooses integers and with . Player keeps secret, and truthfully tells to the player . The player now tries to obtain information about by asking player questions as follows: each question consists of specifying an arbitrary set of positive integers (possibly one specified in some previous question), and asking whether belongs to . Player may ask as many questions as he wishes. After each question, player must immediately answer it with yes or no, but is allowed to lie as many times as she wants; the only restriction is that, among any consecutive answers, at least one answer must be truthful.

Baca lebih lanjut

6 Baca lebih lajut

The International Earth Science Olympiad (IESO): Goals, objectives and syllabus

3. For hundreds of millions of years the atmosphere keeps a more or less similar composition as a result of the mutual relations among the atmosphere with the hydrosphere (oceans), biosphere (photosynthesis and breathing) and the geosphere (gas, volcanic dust and erosion). 4. In the short term human actions cause minimal imbalance in the atmosphere, but in the long term the oceans will become huge sinks that regulate part of the atmosphere

11 Baca lebih lajut

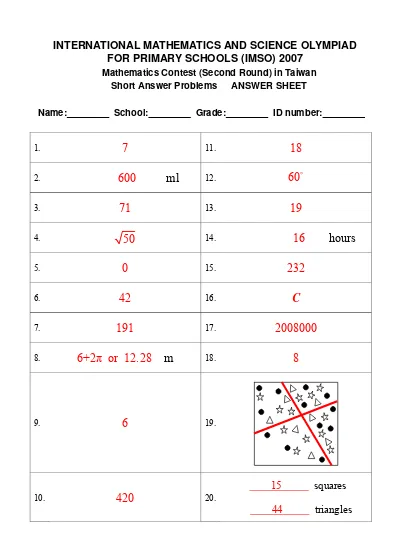
2007IMSO math-Essay

4. Two candles have different lengths and thicknesses. The longer one can burn for 7 hours and the shorter one for 10 hours. After 3 hours' burning, both candles have the same length. What was the shorter candle's length divided by the longer candle's length?

4 Baca lebih lajut

Lecture Notes on Mathematical Olympiad Courses for Junior Section Vol 1 Mathematical Olympiad Series

competitions which students can use to test themselves. These are taken from a range of countries, e.g. China, Russia, the USA and Singapore. In particular, there are many questions from China for those who wish to better understand mathe- matical Olympiads there. The questions are divided into two parts. Those in Part A are for students to practise, while those in Part B test students' ability to apply their knowledge in solving real competition questions.

183 Baca lebih lajut

IMSO 2009 Exploration

6th INTERNATIONAL MATHEMATICS AND SCIENCE OLYMPIAD FOR PRIMARY SCHOOL IMSO 2009 EXPLORATION PROBLEMS Yogyakarta, 8 – 14 November 2009 DIRECTORATE OF KINDERGARTEN AND PRIMARY DEVELOP[r]

4 Baca lebih lajut

t bing 0704752 bibliography

Shriner & Ganguly. 2007. Assessment and Accommodation Issues Under the No Child Left Behind Act and the Individuals with Disabilities Education Improvement Act: Information for IEP Teams. Available on http://aei.sagepub.com/content/abstract/32/4/231.

6 Baca lebih lajut

IMSO 2013 MATH_Essay

10. My twelve-hour clock has four digits, two for the hours and two for the minutes. The minutes are shown with leading 0s, but the hours are not. Upside down, the digits 0, 1, 2, 5, 6, 8 and 9 read 0, 1, 2, 5, 9, 8 and 6 respectively. One day, I made a phone call on the appointed time, and learned that it was too early. Then I realized that I had read the clock upside down. If you know by how much I was early, you will know what time I made the call. What time should I have made the call?

9 Baca lebih lajut

Sari Wijaya 2017 Math Literacy

That mapping has been already initiate by Education and Culture Minister in the research about mathematic literacy skill for student of elementary and secondary school at 2013.the result doesn't far different from PISA result was students mathematic literacy skill still low (Mahdiansyah & Rahmawati, 2014). The research take seven province in Indonesian witch one of them was Daerah Istimewa Yogyakarta (DIY) that based of this research have higher mathematic literacy skill than the other province. However, the domain that have been analyses only the cognitive, content and context. Process domain that was the main component of mathematic literacy doesn't analyses deeply. It underline the needed of student mathematic literacy skill mapping reviewed from process domain.

Baca lebih lanjut

8 Baca lebih lajut

t ing 0807989 chapter1

3 Thus, this present study aims to investigate the students' ability and problems in writing a research proposal. This study has been conducted in an undergraduate English study program in a university in Banten. This study attempts not only to identify the students' ability and problems in writing a research proposal, but also the possible causes of the problems and the possible solutions that can be proposed to solve the problems based on the students' work.

Baca lebih lanjut

6 Baca lebih lajut

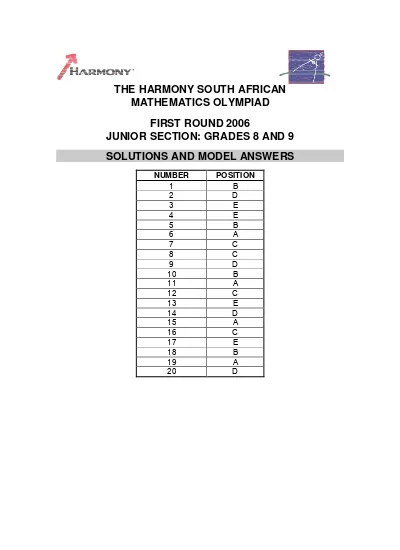
DISINI j1s2006

THE HARMONY SOUTH AFRICAN MATHEMATICS OLYMPIAD FIRST ROUND 2006 JUNIOR SECTION: GRADES 8 AND 9 SOLUTIONS AND MODEL ANSWERS... Suppose she draws 1 more bead.[r]

9 Baca lebih lajut

Mathematical Olympiad Problems And Solutions Pdf

Source: https://123dok.com/title/imomath-th-international-mathematical-olympiad-problems-solutions

Posted by: holleyseentrusels.blogspot.com

Share this post